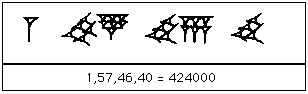इस कहानी का ध्येय- पांचवी पास बच्चों तक अंको का इतिहास बताना| यह बताना स्थानीय मान और चिन्ह मान कितने महत्वपूर्ण होते हैं| भिन्न अंक पद्धतियों के बारे में बताना, उनके विकास की चर्चा करना|
कहानी की पृष्ठभूमि- सौहार्द के बाबा सौहार्द को अंको की कहानी बताते हैं| क्योंकि सौहार्द भिन्न-भिन्न अंको की व्यवस्थाओं से थोडा विचलित है| और जानना चाहता है कि इतनी भिन्न व्यवस्थाएं क्यों हैं|
अम्मा और उनकी सहेली कुछ बात कर रहें हैं-
अम्मा(अपनी सहेली से): ... सोलह आने सच्ची बात...
सौहार्द (बीच में बात काटते हुए): अम्मा, सोलह का सच्ची बात से क्या लेना देना? और ये "आना" क्या होता है?
अम्मा: तुम सवाल बहुत पूछते हो| अपने बाबा से पूछना|
सौहार्द दौड़ कर अपनी माँ के पास जाता है और...
सौहार्द: माँ, बाबा कहाँ हैं? मुझे कुछ पूछना है
माँ: बाबा सब्जियां लेने गए हैं| और सवाल मुझसे मत पूछना, मुझे अभी अम्मा को होली की तारीख/तिथि बतानी है|
सौहार्द (पापा से): पापा-पापा..
सौहार्द (मन ही मन में): ओह पापा तो रद्दी बेच रहे हैं| ये भी कम से कम आधे घंटे से पहले खाली नहीं होंगे| शायद अम्मा की सहेली चली गई हों|
सौहार्द अम्मा के पास पहुँचता है, किन्तु अम्मा तो अब पूजा में तल्लीन हो गई हैं|
सौहार्द (मन ही मन में): अब वे तब तक नहीं उठेंगी जब तक उनके 51 मन्त्र न हो जाएँ और उनके मनके एक बार फिर न जाएँ|
अब सौहार्द को बाबा का ही इन्तजार है| वे ही बताएँगे कि सोलह आने सच्ची बात का क्या मतलब होता है| लो बाबा भी आ गए| अब सौहार्द को चैन कहाँ, तुरंत उसने बाबा पर सारे सवाल दाग दिए|
सौहार्द: बाबा! ये आने क्या होते हैं? सोलह आने सच्ची बात का क्या मतलब होता है? बातों का आने से क्या मतलब होता है?
माँ (सौहार्द की बात बीच में काटते हुए): सौहार्द, पहले बाबा को पसीने सुखा लेने दो, उन्हें पानी पिलाओ फिर अपने सवालों का अम्बार लगाना|
सौहार्द ने पंखा चला कर रेगुलेटर को सबसे तेज कर दिया, बाबा से सब्जियों का थैला ले लिया और उसे रसोई में रख आया| उसने बाबा को पानी दिया, और बाबा के जवाब बताने का इंतज़ार करने लगा|
बाबा ने पानी पिया और सौहार्द के सवालों के लिए तैयार हो गए|
बाबा: तुम्हारा पहला सवाल- “आना क्या होता है?”
बाबा: जैसे आज हम रूपये काम लेते हैं, पहले हमारे देश में मुद्रा के रूप में आने चलते थे| (रूपये जो हमारे देश की मुद्रा है, पहले इसका स्वरुप कुछ भिन्न था तथा वह सोलह आनों में विभाजित होता था|)
Figure 1भारतीय प्राचीन मुद्रा [स्रोत: https://garampakora.blogspot.com/2016/04/cowrie-damri-dhela-pie-paisa-rupyya-and.html]
बाबा: तुम्हारा दूसरा सवाल “सोलह आने का क्या मतलब होता है?” सोलह आने का मतलब सौ फीसदी होता है| जैसे सोलह आने सच्ची बात का मतलब हुआ सौ फीसदी सच्ची बात|
बाबा: और अब तुम्हारा तीसरा सवाल जिसे मै थोडा बदलकर बनाता हूँ- “सोलह आने का मतलब सौ फीसदी क्यों होता है?”
सौहार्द: हाँ हाँ! बाबा यह तो बहुत जरुरी सवाल है|
बाबा: भारत में अंग्रेजों के समय जो मुद्रा चलती थी उसमे आना, रुपया, पैसा और पाई होते थे| एक रूपए में सोलह आने, और एक आने में चार पैसे या बारह पाई होती थी| इस तरह सोलह आने का एक रूपये होता था, जो कि रुपये की पूरा करती थी| इसलिए किसी बात की सत्यता को कहने के लिए हम सोलह आने या सौ फीसदी बोलते हैं|
बाबा: तुम्हे पता है, सन् 1957 में हमने इसमें दशमलव प्रणाली अपना ली| इस कारण जहाँ पहले एक रूपए में चौसठ पैसे होते थे| इसके बाद एक रूपए में सौ पैसे हुए|
सौहार्द: अच्छा बाबा इसलिए ही क्या पचास पैसे के सिक्के को अठन्नी बोलते हैं, और पच्चीस पैसे के सिक्के को चवन्नी|
बाबा: बिलकुल ठीक! सही समझ रहे हो|
सौहार्द: बाबा, ये दशमलव प्रणाली क्या होती है?
बाबा: बेटे, दशमलव प्रणाली में दस भिन्न चिन्ह होते हैं, जैसे हमारी आज की अंक पध्दति में 0,1,2,3,4,5,6,7,8 और 9 हैं| सभी संख्याएं इन्ही दस चिन्हों से प्रदर्शित की जाती हैं|
सौहार्द: बाबा अब तो सिर्फ दशमलव प्रणाली ही चलती है| है न?
बाबा: यहाँ तुम गलती कर गए| किन्तु यह भी सत्य है कि अब जितनी भी मानक इकाई बनाई गई हैं उनमे से ज्यादातर जगह दशमलव प्रणाली ही काम आती है| जैसे हजार मीटर का एक किलोमीटर, या सौ सेंटीमीटर का एक मीटर या सौ पैसे का एक रुपया या हज़ार ग्राम का एक किलोग्राम आदि|
सौहार्द: लेकिन बाबा आपने यह नहीं बताया कि कौन-कौन सी अंक पद्धतियाँ अब भी प्रचलित हैं?
बाबा: अच्छा, यह बताओ कंप्यूटर कौन सी अंक पद्धति को काम लेता है?
सौहार्द: वह तो सिर्फ दो तरह के सिग्नल ही समझता है- वोल्टेज और नो वोल्टेज|
बाबा: हाँ, इसलिए ही वह द्विधारी यानी बाइनरी अंक पद्धति पर काम करता है|
सौहार्द: बाबा हम इतनी देर से बार बार अंक पद्धति शब्द का इस्तमाल कर रहें हैं, यह क्या है?
बाबा: कुछ ख़ास नहीं, जैसे तुम कह रहे हो दशमलव अंक पद्धति में दस, सौ, हज़ार, यानी दस की घात (power) वाली संख्याओं से बड़ी इकाई बनती है उसी तरह तुम किसी और संख्या को भी ले सकते हो|
सौहार्द (रुआंसा होते हुए): बाबाSS ठीक से बतलाओ न| जब भी आप “कुछ ख़ास नहीं” बोलते हो, तब उसके पीछे की रोचक कहानी सुनाते हो|
बाबा: चलो मै तुम्हे अंक पद्धति के विकास की कहानी बताता हूँ|
सौहार्द (ख़ुशी से): हुर्रे!!! बाबा ये हुई न बात|
बाबा: किन्तु, तुम्हे इस पर मुझे निबंध लिख कर देना होगा|
सौहार्द: हाँ बाबा, बिलकुल लिखूंगा|
बाबा: अच्छा यह बताओ कि तुम गिनती कैसे करते हो?
सौहार्द: उँगलियों की सहायता से| जब गिनती कम हो तब उँगलियों से, और बड़ी गिनती हो तब उँगलियों के पोरों से|
बाबा: ठीक इस प्रकार ही आदिम मनुष्य, जिसे संख्याओं के नाम नहीं पता थे, भी गणना करता था| वह उन्हें पोरों जैसी चीज यानी कौड़ियों या पत्थरों की सहायता से गिनता था|
सौहार्द: वह कैसे बाबा?
बाबा: मानलो तुम एक ग्वाले हो
सौहार्द (शरारती अंदाज़ में): कृष्ण जैसे!
बाबा (हँसते हुए): हाँ हाँ, कृष्ण जैसे| (थोड़े कठोर अंदाज में) लेकिन इस कृष्ण को अभी गिनती नहीं आती|
सौहार्द: अच्छा ठीक है|
बाबा: तुम रोजाना गाय चराने जाते हो| जंगल में गायों को ले जाकर उन्हें चरने छोड़ देते हो| खुद खूब खेलते हो, पेड़ो की ठंडी छाँव में सो जाते हो| फिर शाम को उन्हें जंगल से हांक कर ले आते हो|
सौहार्द: कितने मजेदार बात है न| खूब खेलो, सो जाओ .. ये तो बड़ा मजेदार काम है|
बाबा: हाँ, सो तो है किन्तु उतना ही जिम्मेदारी भरा भी|
सौहार्द (परेशान हो कर): कैसे बाबा?
बाबा: क्यों जंगल में तुम्हारी गाय कोई चोरी कर ले गया तो? वह दूर कही चरने चली गयी तो?
सौहार्द: हाँ, यह तो बहुत जिम्मेदारी वाला काम है|
बाबा: किन्तु उससे भी पहले यह ग्वाले के लिए जरुरी है कि वह पहचान पाए कि उसकी गायें कम हो गई|
सौहार्द: हाँ और उसे तो गिनती भी नहीं आती|
बाबा: बिलकुल!!
सौहार्द बाबा को देख आश्चर्य से सोचने लगा| फिर बोला
सौहार्द: बाबा बताओ वे, ऐसा क्या करते थे?
बाबा: वे प्रत्येक गाय के लिए एक पत्थर रख लेते थे| शाम के समय, जब उन्हें वापस लौटना होता, तब अपनी गायों की गिनती पूरी करने के लिए, उन पत्थरों से गायों का मिलान करते| यदि सभी गायों के लिए एक एक पत्थर मिल जाए, तब ग्वालों के पास पूरी गायें हैं|
सौहार्द: और यदि पत्थर बच जाएँ तो गायें पहले से कम हो गई हैं और उन्हें तुरंत ढूंढना चाहिए| है न बाबा?
बाबा: हाँ|
सौहार्द (शरारती मुस्कान लेते हुए, पाठकों से सवाल पूछता है): यदि पत्थर कम पड़ जाएँ, तब उसका क्या मतलब होगा?
बाबा: बेटे, तुम्हे पता है, आज भी हम लोग इस तरीके का इस्तेमाल करते हैं| विशेषत: तब, जब हमें गणना के साथ कुछ और भी करना हो, और हमारे लिए गणना पर ध्यान रखना संभव न हो|
सौहार्द: हाँ बाबा मै जानता हूँ| अम्मा अपने मनको की माला से यही तो करती हैं| चूँकि मन्त्र पढ़ते हुए वे उनकी गिनती नहीं कर पाती इसलिए एक-एक मनका खिसकाती जाती हैं| इससे उन्हें मन्त्रों की गणना भी नहीं करनी पड़ती और वे ठीक 51 बार मन्त्र जाप कर लेती हैं|
बाबा: बिलकुल ठीक! यही नहीं बड़े बड़े गणितज्ञ इस तरीके को इस्तमाल करते हैं, इसे वे one to one correspondence कहते हैं| इसी सिद्धांत से हम ज्यादा या कम पता करने की कोशिश करते हैं, हम देखते हैं कि पत्थर ज्यादा हैं, या गाय| इस सवाल को गणितज्ञ More buttons or button holes अथवा pigeonhole सिद्धांत से भी जानते हैं|
सौहार्द: बाबा फिर क्या हुआ?
बाबा: जैसे-जैसे ग्वाले के यहाँ समृधि आई, उसकी गायें बहुत बढ़ गईं| ग्वाले को गायों को चर्वाने के लिए नौकर रखने पड़े| और नौकर चोरी न करें इसके लिए
सौहार्द(बाबा की बात काटते हुए): उसे ढेरों पत्थरों को रखना पड़ेगा|
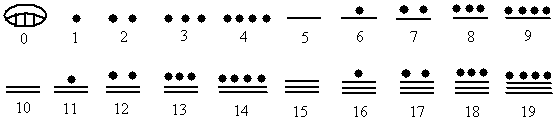
बाबा: हाँ, और इतने पत्थरों को रखना कठिन होने लगा| तब इसके लिए मनुष्य ने चिन्हों का इस्तमाल शुरू कर दिया| वह इन्हें शिलाओं या लकड़ी पर उकेर लेते| निम्न चित्र की तरह|
Figure 2: tally मार्क्स
सौहार्द: यह तो बहुत सुन्दर उपाय लगाया|
बाबा: यह देखो दुनिया भर में भिन्न भिन्न सभ्यताओं ने कौन कौन से चिन्ह इस्तमाल किये थे|
Figure 3:माया सभ्यता [स्रोत: https://www.basic-mathematics.com/mayan-numeration-system.html ]
Figure 4मिस्र सभ्यता [स्रोत: https://discoveringegypt.com/egyptian-hieroglyphic-writing/egyptian-mathematics-numbers-hieroglyphs/ ]
|
character |
numerical value |
|
I |
1 |
|
V |
5 |
|
X |
10 |
|
L |
50 |
|
C |
100 |
|
D |
500 |
|
M |
1000 |
|
# |
RN |
# |
RN |
# |
RN |
|
1 |
I |
11 |
XI |
21 |
XXI |
|
2 |
II |
12 |
XII |
22 |
XXII |
|
3 |
III |
13 |
XIII |
23 |
XXIII |
|
4 |
IV |
14 |
XIV |
24 |
XXIV |
|
5 |
V |
15 |
XV |
25 |
XXV |
|
6 |
VI |
16 |
XVI |
26 |
XXVI |
|
7 |
VII |
17 |
XVII |
27 |
XXVII |
|
8 |
VIII |
18 |
XVIII |
28 |
XXVIII |
|
9 |
IX |
19 |
XIX |
29 |
XXIX |
|
10 |
X |
20 |
XX |
30 |
XXX |
Figure 5रोमन अंक [स्रोत: https://mathworld.wolfram.com/RomanNumerals.html]
बाबा: हाँ, किन्तु तुम सोचो ... यदि पुन: गायें और भी ज्यादा बढ़ जाएँ, जैसे एक हज़ार गायें हो तब क्या होगा|
सौहार्द: ऐसे में तो गलतियाँ बढ़ जायेंगी| एक हजार चिन्ह बनाते हुए बेहद ध्यान रखना होगा यही नहीं उनका मिलान करते हुए भी|
बाबा: बात सिर्फ यही नहीं ख़त्म होती, यदि संख्याएं और भी बढ़ जाएँ तो शिलाएं और लकड़ियों का भी जमकर उपयोग होगा, उनका रख रखाव मुश्किल होगा| तो बताओ इस समस्या से तुम इन मनुष्यों की मदद कैसे करोगे?
सौहार्द: बाबा, क्या कुछ और चिन्ह इस्तमाल करने से कोई फायदा होगा?
बाबा: तुम सही दिशा में हो| अलग अलग सभ्यताओं में और चिन्हों का इस्तमाल किया जाने लगा| ये चिन्ह पांच, दस, बीस, पचास, साठ आदि भिन्न संख्याओं के लिए बनाए गए| जैसे कि तुम fig. 2-4 में देख सकते हो|
बाबा: क्या तुम सोच सकते हो कि गणना करने मे इन पद्धतियों की क्या कमियाँ थी, या ये क्यों वैज्ञानिक प्रयोग के लिए अथवा आम उपयोग के लिए अच्छी नहीं थी|
सौहार्द: बाबा, किन्तु मेरा भी एक सवाल है?
बाबा: अच्छा तुम पहले पूछो|
सौहार्द: इन पद्धतियों मे हम जमा, घटाव, गुणा भाग आदि आधारभूत गणनाएं कैसे करते हैं?
बाबा: तुम बहुत चतुर हो, तुमने मेरे सवाल को भी अपने सवाल मे मिल लिया|
सौहार्द: क्या मतलब?
बाबा: सौहार्द, इन पद्धतियों में इन गणनाओं को करना एक कठिन कार्य होता है| जिस प्रकार तुम पहाड़े याद करते हो| और 0-9 तक के पहाड़े याद करना बहुत जरूरी होता है| अंदाज लगा सकते हो क्यों?
सौहार्द: क्योंकि हम दस चिन्हों का प्रयोग करते हैं| क्या यह कारण सही है? ओह, तब उपरोक्त पद्धतियों के तो बहुत सारे पहाड़े याद करने होंगे|
बाबा: बिल्कुल सही| और तुम देख सकते हो कि उपरोक्त सभी पद्धधतियों में संख्या के मान के साथ चिन्ह भी बढ़ते ही चले जाते हैं| अत: इनके पहाड़ों का भी कोई अंत नहीं होगा|
बाबा: अच्छा क्या तुम बता सकते हो कि इन चिन्हों के क्रम में बदलाव करने से संख्या में कोई अंतर पड़ेगा?
सौहार्द: नहीं, ठीक नोटों (मुद्रा पत्रों/currency notes) की तरह| जिनको किसी भी क्रम में रख लो उनकी कीमत वही रहती है| सही कह रहा हूँ न बाबा|
बाबा: किन्तु फिर भी तुम देख सकते हो, सभी सभ्यताओं को क्रम की समझ थी इसलिए भिन्न संख्याओं को दर्शाने वाले चिन्हों को क्रमवार रखा जाता था|
सौहार्द: हाँ, ठीक ऐसे ही जैसे आप और पापा नोटों (मुद्रा पत्रों/currency notes) को क्रमवार रखना पसंद करते हो|
बाबा (हँसते हुए): बिल्कुल ठीक पकड़ा|
सौहार्द: लेकिन बाबा, पांच हजार लिखने के लिए हजार के चिन्ह को पांच बार लिखने की जगह पांच का चिन्ह और हजार का चिन्ह भी तो लिखा जा सकता है|
बाबा: हाँ, सही ऐसा भी\ कई सभ्यताओं में किया गया|
बाबा: किन्तु, बेबिलोनियन सभ्यता के निवासियों ने पहली बार स्थान की महत्ता शुरू करते हुए हजार का, दस का चिन्ह ही हटा दिया सिर्फ यह लिखा की वह चिन्ह कितनी बार लिखा जाना चाहिए| जैसे-`
Figure 6बेबीलोनीयन सभ्यता [स्रोत: https://mathshistory.st-andrews.ac.uk/HistTopics/Babylonian_numerals/]
Figure 7: बेबीलोनीयन सभ्यता स्थान महत्ता [स्रोत: https://mathshistory.st-andrews.ac.uk/HistTopics/Babylonian_numerals/]
1×603+57×602+46×60+40 = 424000
सौहार्द: लेकिन बाबा, तब क्या होगा जब किसी स्थान के लिए हमारे पास कोई संख्या ही न हो?
बाबा: तुम्हारी चिंता जायज है, बेबिलोनियन सभ्यता में ऐसे स्थान को लोग खाली छोड़ देते थे|
सौहार्द: किन्तु, क्या इससे गलतियाँ होने की संभावना नहीं बढ़ेगी, जैसे मान लीजिये-
बाबा: इसका जवाब हिन्दू सभ्यता ने शून्य देकर किया| यहाँ सर्वप्रथम खाली स्थान को शून्य के चिन्ह से भर दिया गया|
सौहार्द: और हिन्दू सभ्यता के यही अंक सारी दुनिया में अरब के रास्ते फ़ैल गए| यह तो बेहद रोचक कहानी है| बाबा इसे मै भी अपने दोस्तों को सुनाऊंगा|